Особенности теплового расчета импульсных силовых каскадов

Бурное развитие силовой преобразовательной техники, происходящее в настоящее время, неразрывно связано с появлением на рынке полупроводников новых компонентов, обладающих уникальными импульсными характеристиками. В первую очередь это силовые транзисторы MOSFET и IGBT. Использование этих компонентов в мощных приводах, источниках питания и других подобных устройствах позволяет создавать преобразователи, имеющие высокую эффективность и отличные массогабаритные показатели. Отсутствие тока управления в статических режимах дает возможность отказаться от схем управления на дискретных компонентах и использовать интегральные схемы управления — драйверы. Такие микросхемы выпускаются сейчас почти всеми ведущими производителями силовой электроники. Они способны управлять транзисторами и модулями в любой конфигурации и кроме выработки сигналов управления осуществляют все необходимые вспомогательные функции: защиту от перегрузки по току и короткому замыканию, защиту от падения управляющего напряжения, формирование контрольных сигналов.

В результате быстрого развития технологии мощных полупроводниковых приборов, драйверов и микроконтроллеров, осуществляющих управление системой, понятие схемотехника как искусство создания принципиальной схемы утратило свое первоначальное значение. Разработчику силового каскада требуется «всего лишь» грамотно выбрать ключевой элемент и драйвер для управления им, пользуясь соответствующими цифрами и графиками. Однако это «всего лишь» иногда оказывается серьезной проблемой. Предельные данные тока и напряжения транзистора или модуля, обычно вынесенные в отдельный подзаголовок технических характеристик, не дают разработчику никаких данных для расчета, а позволяют только в первом приближении сравнить один элемент с другим. Сложность выбора компонента заключается в том, что желательно максимально использовать его мощностные характеристики, чтобы не платить лишних денег за неоправданный запас по мощности. Проблему также представляет и выбор драйвера, который должен быть грамотно согласован с силовым элементом по току затвора, управляющему напряжению и динамическим характеристикам.

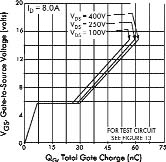
Рис. 1. Зависимость заряда затвора от напряжения на затворе для транзистора IRF840

Большие значения допустимых импульсных токов (они могут в 5–10 раз превышать значение среднего тока) создают у разработчика иллюзию, что транзисторы могут работать в режиме перегрузки. На самом деле перегрузка совершенно недопустима. И для оценки правильности выбора элемента существует только один критерий — температура кристалла в наиболее напряженном режиме работы. Тепловой анализ работы силового каскада состоит из трех этапов: расчет мощности потерь, расчет температуры кристалла полупроводника и выбор теплостока. Предлагаемая статья ставит своей задачей помочь разработчику решить эту проблему.

Мощность потерь

Методика расчета мощности рассеяния импульсных силовых компонентов приводится во многих инструкциях по применению и сводится она, как правило, к нахождению суммы статических и динамических потерь. Однако эти расчеты различаются для разных конфигураций схем, поэтому представляется полезным привести формулы, необходимые для инженерных расчетов, в предлагаемой статье. Расчет должен производиться для наиболее тяжелого режима работы, т. е. когда через транзистор течет предельный ток и коэффициент заполнения — максимален. Напомним, что коэффициент заполнения (в англоязычной литературе он называется Duty Factor и обозначается буквой D) — это отношение длительности импульса проводимости к периоду повторения импульсов, т. е. это величина, обратная скважности. Формулы даны для режима «тяжелого переключения», когда коммутируется одновременно полный ток и напряжение. Как будет показано далее, температуры кристалла определяется с помощью графика теплового импеданса. Исходными данными для расчета являются значение мощности потерь за импульс проводимости (время внутри периода ШИМ, в течение которого через транзистор течет ток) и температура корпуса элемента.

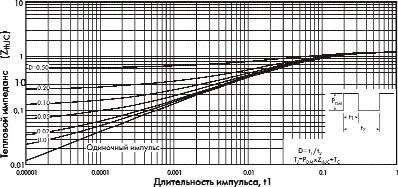
Рис. 2. Значение теплового импеданса при различных значениях длительности импульса проводимости t1 и коэффициента заполнения D для транзистора IRGS14C40L

A. Мощность статических потерь транзистора MOSFET

P_D1=I²_DavxR_DS(on) (1)
IDav — среднее значение тока стока за время импульса проводимости;
R_DS(on) — сопротивление открытого канала.

B. Мощность статических потерь транзистора IGBT

P_D2=I_cavxU_ce(@I_c) (2)
I_cav — среднее за время импульса проводимости значение тока коллектора
U_ce(@I_c) — напряжение насыщения при данном токе коллектора, определяется из графика U_ce=f(Ic), приводимого в технических данных.

С. Мощность динамических потерь транзистора MOSFET без учета тока обратного восстановления оппозитного диода.

Примечание: формула используется для однотактных схем с чисто активной нагрузкой, когда нет влияния тока обратного восстановления оппозитного диода и отсутствует ток через внутренний антипараллельный диод транзистора.
Оппозитный (opposite) диод — диод противоположного плеча полумоста или диод в чопперной схеме.

Антипараллельный (antiparallel) диод — внутренний диод MOSFET (body diode) или встроенный диод IGBT.

P_SW1=(2xU_sxI_dxQ_g/I_g)xF (3)
I — максимальный ток стока;
Us — напряжение питания;
Qg — полный заряд затвора;
F — частота переключения;

Ток затвора I_g можно примерно определить как отношение разности максимального напряжения на затворе U_gs и напряжения, соответствующего заряду емкости Миллера Ugm к импедансу схемы управления затвором. Значение импеданса включает в себя выходное сопротивление драйвера и резистора затвора.

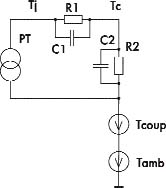
Рис.3. Эквивалентная электрическая схема

I_g=(U_gs — U_gm)/R_g (4)
Напряжение U_gm определяется по горизонтальному участку на графике V_gs=f(Qg). Например, для IRF840 U_gm » 5В (рис. 1).

D. Мощность динамических потерь транзистора IGBT

Примечание: значение энергии Ets учитывает потери от обратного восстановления оппозитного диода и потери, вносимые за счет «хвоста» — остаточного тока коллектора выключенного транзистора.
P_SW2 = E_ts(@I_c@R_g)xF (5)
E_ts(@I_c@R_g) — суммарная энергия потерь с учетом тока коллектора и импеданса цепи управления затвором. Определяется по графикам E_ts = f(R_g) и E_ts = f(I_c).

Е. Мощность динамических потерь транзистора MOSFET с учетом тока обратного восстановления оппозитного диода Примечание: оппозитный диод имеет характеристики проводимости и восстановления, соответствующие характеристикам внутреннего диода полевого транзистора, как это имеет место в полумостовых и мостовых схемах.
P_SW3=U_sx(I_dxt_a+0,5Q_rr)xF (6)
I_d — максимальный ток стока;
t_a — составляющая времени обратного восстановления t_rr, пока напряжение на диоде остается близким к 0 (примерно равно времени включения транзистора ton);
t_on=Q_g/I_g — значение I_g рассчитывается, как показано выше;
Q_rr — заряд обратного восстановления оппозитного диода.
Автору неизвестны точные формулы для оценки динамических потерь с учетом тока обратного восстановления диода полевого транзистора. Выражение Е выведено с учетом некоторых упрощений, однако для инженерного теплового расчета его точности вполне достаточно.

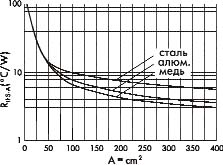
Рис. 4. Зависимость теплового сопротивления RthSA от площади плоской пластины для различных материалов

F. Мощность, рассеиваемая на антипараллельном диоде

Примечание: на внутреннем диоде транзистора MOSFET или на встроенном диоде транзистора IGBT мощность рассеивается при коммутации тока в индуктивной нагрузке. Прирост температуры кристалла за счет рассеяния мощности на антипараллельном диоде должен рассчитываться отдельно, т. к. тепловое сопротивление RJC для диода часто отличается от значения RJC для транзистора.
P_DF = I_FMxV_FM(@I_FM) (7)
I_FM — средний ток диода;
V_FM(@I_FM) — напряжение на диоде при токе I_FM.

G. Мощность, рассеиваемая в режиме синусоидальной модуляции

В каскадах, где выходной ток меняется по синусоидальному закону, вычисление мощности потерь оказывается наиболее сложным. Инвертор с изменяющимся током обычно называют VVVF-инвертор (variable voltage variable frequency). В VVVF-устройствах скважность импульсов управления изменяется по синусоидальному закону. Потери в VVVF-инверторе зависят от температуры, частоты ШИМ, скважности, величины тока пульсаций и других факторов. Для приблизительной оценки мощности потерь в данном случае можно воспользоваться рекомендациями фирмы Mitsubishi [7]:

Потери в IGBT:
P_D=I_CPxV_satx(1/8+D_Mxcosq/3¶) (8)
— статические потери
P_SW=E_ts(@I_c@R_g)xF/p (9)
— динамические потери
P_DM=P_D+P_sw (10)
— суммарные потери
Потери в диоде:
P_DF= I_FMxV_FM(@I_FM)x(1/8 — Dxcosq/3¶) (11)
— статические потери
P_rr = 0,125xI_rrxt_rrx V_SxF (12)
— потери за счет восстановления

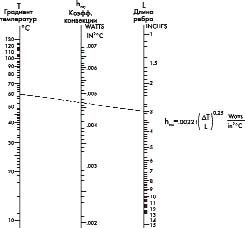
Рис. 5. Номограмма для радиатора с вертикальными ребрами при естественном охлаждении м

Суммарные потери на плече:
P_A = P_DM + P_DF + P_rr . (12)
Мощность, рассеиваемая на 3-фазном усилителе, будет, соответственно, в 6 раз больше.
q — угол между напряжением и током;
cosq — коэффициент мощности (Power Factor);
I_CP — пиковое значение синусоидального выходного тока;
D_M — глубина модуляции;
V_FM(pk) — пиковое значение напряжения на диоде при восстановлении;
I_rr — пиковый ток обратного восстановления;
t_rr — время обратного восстановления диода
V_S — напряжение питания силового каскада
Таким образом, пользуясь приведенными формулами, мы можем найти суммарную мощность потерь Pе практически для любой конфигурации схемы:
P_е= P_D + P_SW + P_DF (13)
Дальнейшим шагом будет нахождение температуры кристалла.

Температура кристалла

В справочных данных на любой силовой транзистор или модуль обязательно приводится график теплового импеданса Z_thJC(⁰С/Вт), подобный показанному на рис.2. С помощью этого графика, зная суммарную мощность потерь PDM за время импульса проводимости t₁, коэффициент заполнения D и температуру корпуса элемента T_c, можно определить температуру кристалла TJ:

Нижний график дан для одиночных импульсов, при которых допустимый ток максимален. Эта эпюра может быть использована, например, для расчета режима защиты от короткого замыкания. С ее помощью можно определить допустимый пиковый ток короткого замыкания и минимальное время отключения транзистора при циклическом характере работы схемы защиты.

В формуле (14) есть одна неизвестная величина — температура корпуса транзистора (модуля) Тс. Она определяется по формуле:
Tc= Pе x D xR_thCS+T_s= Pе x D x R_thCS+ Pе x D x R_thSA+T_a (15)
где:
Pе x D — средняя рассеиваемая мощность;
R_thCS — тепловое сопротивление корпус транзистора — теплосток;
R_thSA — тепловое сопротивление теплосток–окружающая среда;
T_a — температура окружающей среды;
T_s — температура теплостока.

В данной формуле нам неизвестно значение T_s (или R_thSA). Однако, если выходной каскад работает не в очень напряженном тепловом и электрическом режиме, размер радиатора не ограничен и обеспечен отвод тепла, то для расчета можно воспользоваться простой инженерной формулой — площадь излучающей поверхности теплостока St должна быть:

St > 20 x Pе x D (см2)

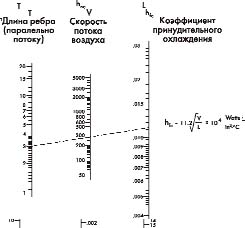
Рис. 6. Номограмма для радиатора с принудительным охлаждением

При этом перегрев поверхности радиатора над окружающей средой не превысит 35°С: T_s = T_a + 35°С
. Для более сложных случаев необходим серьезный анализ, методика которого приводится ниже.

Общие положения

Основные потери в силовых транзисторах и модулях создаются непосредственно в кристалле. Тепло, выделяемое полупроводниковым кристаллом, отводится через корпус элемента на теплоотвод и далее в окружающую среду. При рассмотрении методов теплопередачи должны быть рассмотрены три основных процесса: теплопроводность, теплоизлучение и конвекция. В процессе охлаждения в зависимости от способа отвода тепла любой из этих процессов может доминировать. Например, если охлаждаемое устройство установлено на теплосток с жидкостным охлаждением, большая часть тепла отводится за счет теплопроводности. При использовании вентиляторов в режиме принудительного охлаждения основное тепло отводится за счет конвекции. Для большинства индустриальных применений охлаждение с помощью естественной или принудительной вентиляции применяется чаще всего, и именно эти методы будут рассмотрены далее.

Тепло от кристалла отводится прежде всего через материалы, находящиеся в непосредственном контакте с ним, т. е. корпус элемента и теплоотвод. Поскольку теплоотвод имеет конечные размеры, его температура всегда выше температуры окружающей среды. Эта разница зависит от размера, формы, материала радиатора и способа охлаждения (естественная или принудительная вентиляция, жидкостное охлаждение). Целью всегда является ограничение температуры кристалла на допустимом уровне.

Условие температурной стабильности системы «силовой модуль — окружающая среда» при известном значении теплового сопротивления кристалл — окружающая среда R_thJA может быть описано следующим соотношением:

d_PD/d_TJ< 1/R_thJA , (16)
где:
d_PD/d_TJ — изменение рассеиваемой мощности на единицу изменения температуры кристалла.
Тепловое сопротивление R_thJA обычно содержит три составляющих: R_thJC (сопротивление кристалл–корпус элемента), R_thCS (сопротивление корпус–теплосток) и RthSA (сопротивление теплосток–окружающая среда).

R_thJA= R_thJC + R_thCS + R_thSA (17)
Из приведенных выражений можно определить температуру кристалла TJ при известных значениях рассеиваемой мощности P и температуры окружающей среды T_A.

T_J = T_е+ P*R_thJA (18)
Для теплового анализа с помощью программ схемотехнического моделирования (например, PSPICE) может быть использована эквивалентная электрическая схема, приведенная на рис. 3.

Р_T — расчетные потери, представленные источником тока; R₁ — тепловое сопротивление «кристалл — корпус» с учетом тепловой постоянной времени, задаваемой емкостью С1; R₂, C₂ — определяют тепловое сопротивление и тепловую постоянную времени радиатора; T_j — температура кристалла; T_c — температура корпуса транзистора (модуля).

Источники напряжения используются для установки температуры окружающего воздуха T_amb и для учета эффектов тепловой связи в модулях T_coup.

Описанная тепловая модель пригодна для вычисления средней температуры перегрева кристалла в установившемся состоянии. Необходимые для расчета значения R_thJC и R_thCS являются параметрами силового компонента или модуля и указываются в технических характеристиках, а R_thSA — параметр теплостока.

Тепловые сопротивления RthJC и RthCS

Температурный градиент, возникающий на переходе кристалл–корпус элемента, зависит от размеров, формы и материала теплопроводящего основания корпуса — базовой поверхности, свойств компаунда, крепящего кристалл к корпусу. Сопротивление R_thJC — это технологический параметр, и для его снижения производители компонентов разрабатывают новые типы корпусов, новые материалы, оптимизируют размеры кристалла и способы крепления кристалла к корпусу. Например, для транзисторов фирмы International Rectifier в корпусе SuperTO-247 сопротивление R_thJC = 0,36 °/Вт. Для транзисторов в корпусе ТО-247, имеющем те же размеры, R_thJC=0,64 °/Вт.

Для достижения минимального значения R_thCS необходимы следующие условия:

• Контактные поверхности модуля и теплоотвода должны быть максимально чистыми, плоскими и гладкими. Рекомендуемое отклонение от плоскости (кривизна поверхности) не более 0,025мм.
• Контакт между модулем и теплоотводом должен быть заполнен теплопроводящим компаундом или пастой, которые вытесняют воздух и обеспечивают надежный и стабильный теплообмен.
• Крепление модуля к теплоотводу должно производиться при определенном вращающем моменте, значение которого указывается в технических характеристиках на модуль. При установке модуля необходимо проконтролировать момент затяжки через 3 часа для лучшего распределения теплопроводящего компаунда в зазоре.

Тепловое сопротивление RthSA

В зависимости от конструкции устройства в качестве теплостока может быть использован специальный радиатор, шасси или корпус устройства. Во всех случаях необходимо обеспечить эффективный отвод тепла от базовой поверхности модуля в окружающую среду, оптимальный тепловой контакт с охлаждающей поверхностью и высокую теплоемкость радиатора для исключения локального перегрева при кратковременных перегрузках.

Из материалов, применяемых для изготовления радиаторов, наиболее высокими значениями теплоемкости на единицу объема обладают сталь, медь, латунь, алюминий. По теплоемкости на единицу веса лучшие характеристики имеют никель и алюминий.

Самую высокую теплопроводность из доступных материалов обеспечивают медь, алюминий и латунь. Если не думать о весе радиатора, то наибольшая теплоемкость у никеля, однако на практике алюминиевые радиаторы предпочтительнее с точки зрения соотношения эффективности теплоотдачи на единицу объема.

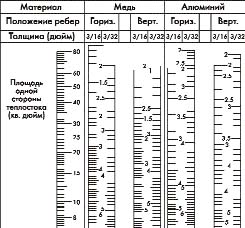
Рис. 7. Тепловое сопротивление RthSA в зависимости от размеров теплостока

На рынке сейчас имеются алюминиевые теплоотводы различных форм и размеров. Как правило, производители радиаторов определяют тепловое сопротивление радиатора как функцию геометрических размеров и рассеиваемой мощности.

При разработке собственного радиатора или использовании в качестве теплоотвода корпуса прибора значение RthSA может быть определено, как функция площади излучающей поверхности и коэффициента теплопередачи.

Упрощенное выражение, которое учитывает вклад всех трех основных способов теплоотдачи (т.е. теплопроводность материала радиатора, конвекцию и излучение), приведено ниже [8]:

R_thSA=l1/k_thA₁ + 1/(h_cA₂ + h_rA₃), (19) где:
k_th — теплопроводность материала радиатора (Вт/ °Сґм2);
l₁ — средняя длина теплового пути, м;
A₁ — средняя площадь сечения, перпендикулярного тепловому пути, м²;
h_c — коэффициент теплопередачи за счет конвекции;
A₂ — площадь теплоотвода, находящаяся в контакте с охлаждающим воздухом, м²;
h_r — коэффициент теплопередачи за счет излучения;
A₃ — эффективная излучающая площадь теплоотвода, м².

Хороший радиатор, разработанный для естественного или принудительного охлаждения, должен обеспечивать низкие потери проводимости (минимум l₁ и максимум A₁), хорошую конвекцию (максимум A₂) и высокую способность к излучению (максимум h_r).

Очевидно, что сопротивление R_thSA падает с ростом охлаждающей поверхности. На рис. 4 приведены графики зависимости R_thSA от площади плоской радиаторной пластины для различных материалов.

Эффективность охлаждения за счет излучения и конвекции

Если отвод тепла производится с помощью плоской радиаторной пластины при естественном охлаждении, коэффициент излучения h_r будет примерно равен коэффициенту конвекции h_с. Когда форма теплостока более сложная, охлаждение за счет конвекции существенно превышает излучение. Это происходит потому, что коэффициент конвекции зависит от общей площади радиатора, а коэффициент излучения — от площади огибающей поверхности.

В реальных условиях разница оказывается еще более значительной из-за того, что обычно только одна сторона теплоотвода способна беспрепятственно излучать тепло. При этом мощность, рассеиваемая за счет излучения, может быть менее 7 % от общего значения. В режиме принудительного охлаждения рассеянием мощности за счет излучения можно вообще пренебречь.

На теплоизлучение большое влияние оказывает качество и цвет поверхности. Для полированного алюминия коэффициент h_r примерно 0,1, для оксидированного алюминия hr может достигать 0,6, матовое покрытие обеспечивает коэффициент h_r в диапазоне 0,7 — 0,8, для черного анодированного матового алюминия h_r » 0,9.

Тепловое сопротивление радиатора не имеет фиксированного значения, поскольку зависит от его ориентации и температуры окружающей среды. Например, вертикальное расположение ребер усиливает теплообмен. Радиатор должен быть расположен так, чтобы не было препятствия для отвода горячего воздуха и не было дополнительного нагрева от окружающих источников тепла.

Более эффективная теплоотдача обеспечивается при принудительном охлаждении с помощью вентиляторов, использование которых позволяет резко снизить тепловое сопротивление. На рис. 5 и 6 показаны номограммы и формулы для расчета радиатора в режиме естественного и принудительного охлаждения, на рис. 7 — номограммы для расчета R_thSA как функции размеров теплоотвода.

На номограммах приняты следующие обозначения:
h_nc — коэффициент теплопередачи для естественного охлаждения;
D_T — градиент температуры радиатор–окружающая среда;
L — вертикальная длина ребра при естественном охлаждении или длина ребра, параллельного потоку воздуха при принудительном охлаждении;
h_fc — коэффициент теплопередачи для принудительного охлаждения;
V — скорость охлаждающего потока воздуха.

Все приведенные выше соображения справедливы для установившегося состояния. На практике имеют место также локальные перегревы, возникающие изза тепловых переходных процессов. Перегрев может стать следствием резкого изменения температуры окружающего воздуха или электрической перегрузки. Мощность, рассеиваемая на кристалле при однократной перегрузке, и его температура рассчитывается по известным формулам с учетом графика теплового импеданса Z_thJC для одиночного импульса.

Ниже приведена стандартная последовательность операций, необходимых для теплового расчета силового модуля. Предполагается, что модуль работает в режиме рассеяния некоторой постоянной мощности и периодически подвергается перегрузкам.

• Рассчитываются потери мощности силового компонента в установившемся состоянии. На основании полученного значения и значения теплового сопротивления R_thJC, определяется перепад температуры на переходе кристалл — корпус модуля;
• С помощью теплового сопротивления R_thCS, рассчитывается перепад температуры на переходе корпус модуля–поверхность радиатора;
• Выбирается длина радиатора и скорость охлаждающего воздуха (в режиме принудительного охлаждения), определяется тепловое сопротивление R_thSA для рабочего режима и рассчитывается перепад температуры поверхность радиатора–окружающая среда;
• Сумма найденных тепловых перепадов суммируется с максимально возможной температурой окружающего воздуха и находится максимальная температура кристалла в установившемся состоянии;
• Рассчитывается дополнительная мощность, рассеиваемая в режиме пиковой нагрузки. С помощью графиков теплового импеданса ZthJC определяется перегрев кристалла в этом режиме и суммируется с температурой для установившегося состояния.
• Результирующая температура кристалла сравнивается с допустимой для данного кристалла.
• Находится интервал времени между импульсами перегрузки. Если это время достаточно для охлаждения кристалла до рабочей температуры установившегося значения, расчет на этом заканчивается.
• Если тепловые режимы не обеспечивают безопасной работы, корректируются параметры радиатора, элемент заменяется на более мощный или используется параллельное соединение элементов.

Литература

• А. И. Колпаков. Автоматизация теплового расчета оконечных каскадов на IGBT транзисторах. Экспресс Электроника № 5, 6, 1998.
• А. И. Колпаков. IGBT или MOSFET? Практика выбора. Электронные компоненты №2, 2000.
• Sven Konrad. Тепловые параметры силовых модулей в широтно-импульсных преобразователях. Technical University of Ilmenau, Germany.
• Applications handbook — Power semiconductor devices. International Rectifier, 1995.
• Thermal Impedance of Cooling Fins. E .J. Diebold, W. Luft. AIEE Transactions, 1858.
• An Introduction to the Art of Heat Sinking. W. E. Goldman, Electronic Packaging and Production, 1966.
• General Considerations for IGBT and IPM. Mitsubishi Application Notes.
• Thermal Considerations in the Application of Silicon Rectifier. IR Designer's Manual, 1991.

Андрей Колпаков
kai@megachip.ru